Few things in the sciences have the near-universal power to stoke the fires of contentious scholarly debates than the subject of null hypothesis significance testing – or NHST. Across many scientific disciplines NHST is the standard way in which we determine whether or not our research findings are worth talking about.
Continue readingAh, simulations. The mere mention conjures images of wily statistical wizards from beyond the beyond, fingers flitting about the keyboard bashing out a frenzied stream of code fashioned to render order from the chaos of numerical nothingness.
In reality, it’s not nearly this intense. At least not for you, dear user. Your poor computer however, will have to do most of the heavy lifting. So be sure to thank it for the service.
Anyways, yes… simulating correlated data. A useful but slightly tricky endeavor if you’re new to this sort of stuff. It’s not beyond your means however, so stick with me here and we’ll make some progress. Let’s tackle this one in R.
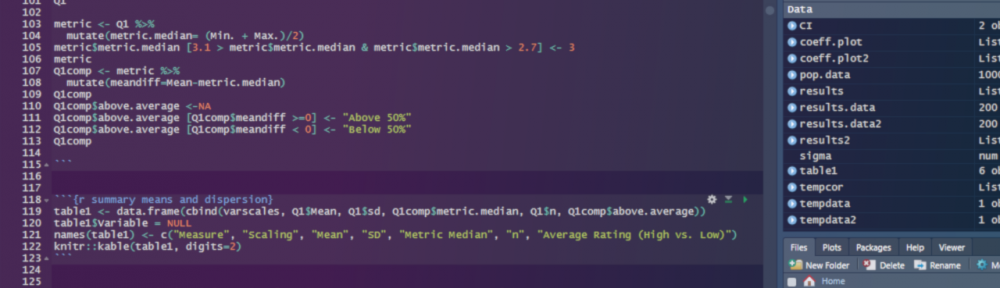
We’ll use the MASS package’s mvrnorm function to quickly and easily generate multiple variables that are distributed as standard normal variables. Here I’m simulating 100 observations, which I define as the value N below (i.e., I’m going to be drawing values randomly from some normally distributed variable in the population 100 times). Next I’m defining two population means for two variables that I’ll simulate for these 100 observations, which I define in a vector called mu (from here on, we’ll just call these variables variable 1 and variable 2 because, let’s be real, it’s past midnight as I’m writing this, and I’m way too tired to be creative about it right now). Lastly, I’m specifying an underlying 2×2 covariance matrix (that I call sigma), which defines the variances of each variable in the population, as well as defining the covariance of both variables in the population. I’ll explain the numbers below after the jump. For now, just peep the code:
#Libraries we'll need:
library (MASS)
N <-100 #setting my sample size
mu <- c(2,3) #setting the means
sigma <- matrix(c(9,6,6,16),2,2) #setting the covariance matrix values. The "2,2" part at the tail end defines the number of rows and columns in the matrix
set.seed(04182019) #setting the seed value so I can reproduce this exact sim later if need be
df1 <- mvrnorm(n=N,mu=mu,Sigma=sigma) #simulate the data, as specified aboveMany students have a difficult time understanding standardization when starting out in learning statistics. Common questions often include:
The answers are fairly straightforward. Here’s a rundown for your statistical woes.
Welcome to another stupidly-long, but hopefully informative instructional on introductory statistical concepts. Today we tackle regression analysis. Use the menu links below to jump around if you need/want to get a quick bit of info on any topic:
Menu
1) Background: Correlation analysis [conceptually] explained
2) Correlation analysis and OLS linear regression
3) From guesses to predictions: The logic of using linear regression
— a) Building the equation
— b) Interpreting regression
— c) What is OLS?
4) Advanced Applications
5) Conclusion & Further reading
I recently set to the task of training undergraduate students in some of the basic data management & analysis procedures available in SPSS. This post consists of the primer that I’ve used to give my research assistants a footing in working with data sets in SPSS, and specifically, how to begin working with the SPSS programming language to create scales, instead of using point-and-click commands to do your work. Up and coming students might find this material useful, as may those of you who are training up new students too. Feel free to pass it along.
“Hello syntax, my old friend.”
Starting new syntax: To open a new syntax editor window, click FILE –> NEW –> SYNTAX. This will open up a blank syntax window that you can begin to write into. The left hand side shows a short list of the major commands in your syntax program. It will auto-update as you write new statements and commands in the main window on the right hand side. You can save syntax files to your hard drive as .sps files. Also note that you can also view the contents of any .sps file using a plain text program like Notepad (Windows) or TextEdit (Mac). This is handy when you just want to see what’s in a syntax file, but don’t have access to SPSS at the moment.
Not too long ago, I wrote an article here about advanced procedures for examining interactions in multiple regression. As I described some of the challenges researchers commonly face in trying to examine differences between people in a data set, I argued that when it comes to data analysis, splitting a continuous variable into a dichotomy (i.e. two categories) is kind of a dumb idea (MacCallum et al, 2002). Continue reading
Today’s tutorial involves picking up a useful new weapon for your data analytic arsenal; one that I’ve used quite a bit over the past year of my graduate training. We’re going to look at a novel way of estimating & graphing interactions in the context of multiple regression (one that even extends to structural equation models), using my increasingly go-to program – Mplus. Note that the tips below have been tested in Mplus versions 6 and 7 effectively. Using these procedures in any earlier version is a total crap shoot — meaning I haven’t verified whether or not they work in version 5 or older — so bear that in mind.
Every field has its landmark papers. You know – the real game changers. In our field, these are often synonymous with those papers that make their way inexorably into almost every single social psychology lecture across the globe (e.g., Milgram, 1963). The papers I’ve listed here are perhaps not quite in that league [yet!]. However, they are papers that I’ve come across in my travels through grad school, to which I’ve found myself returning again and again. Continue reading
Back again with a new Excel tool. This one, which I’ve titled the “Coefficient Cruncher” is a recent development that I’ve been using to write up various sets of results, and it has greatly accelerated my output rate. One of the most tedious things about writing up results is… well, writing up results. This helps.
WITH statement outputs).(Click here for information on the older version 1.2)
The Model Fit Aggregator is a tool I designed for use with Mplus model output. It compiles the results of goodness of fit tests and returns them to the user in easy-to-use APA-style for reporting in manuscripts, talks, posters, etc. It will also compare changes in goodness-of-fit across two nested models. Continue reading
Fred Clavel, Ph.D. 